Some historical cryptography methods

In 1967 David Kahn wrote a book with a title The Codebreakers – The Story of Secret Writing. The book explained the history of cryptography in a very comprehensive and chronological order starting from the ancient Egypt to the time it was written. In his book Khan said “The multiple human needs and desires that demand privacy among two or more people in the midst of social life must inevitably lead to cryptology wherever men thrive and wherever they write.” (Kahn, 1973) (p. 73). According to Kahn the first documented example of written cryptography is done in 1900 B.C. by an anonymous Egyptian master scribe. This master scriber used non-standard hieroglyphs, not fully developed code, to write the life story of the nobleman Khnumhotep II, his master, on the main chamber of his tomb (Kahn, 1973). The intention of the writing was not to make it secret, rather to give it dignity and authority. Even though the script was not secret writing, it was considered as cryptography because it incorporated one of the essential elements of cryptography which is a deliberate transformation of the writing. As the civilization and writing developed in Egypt and more people start to put writings on the tombs, the idea of transformation grew and became more complicated. Ultimately the scribes started to replace the usual hieroglyphic form of a letter to the actual image that can represent the letter, as in English a picture of an eye could represent the letter i or picture of a bee could represent the letter b. Later, the other essential element of cryptology which is secrecy started to be crept in the Egyptian writings and was in use ever since.

Figure 1: The Spartans “Skytale” (Djekic, 2013)

In 487 B.C. the Spartans started to use a device called the “Skytale” to send secret messages in the battlefield. Skytale (figure-1) is consisted of wooden staff and a strip of leather. When they want to write a message, they wrapped the strip of leather close-packed around the staff and wrote the message on the lather down the length of the staff. The lather was then unwrapped form the staff and is sent to the receiver concealed as a belt by the deliverer (Djekic, 2013). To get the original message back the receiver has to rewrap the lather strip around a staff of the same thickness. This technique of cryptography can be categorized as symmetric key cryptography, as both the sender and receiver has to have the staff of specific thickness as their secret key to unwind the cipher to its original message.

Polybius square is another historic cryptography introduced by the Ancient Greek historian Polybius (203-120 B.C.). Polybius technique was to substitute letters with numbers. He arranged the Latin alphabets in a 5×5 square matrix with each alphabet being represented by its row and column number as it is shown in table-1. His technique was widely adopted as cryptographic method (Tabu S. Kondo, Leonard J. Mselle, 2013).

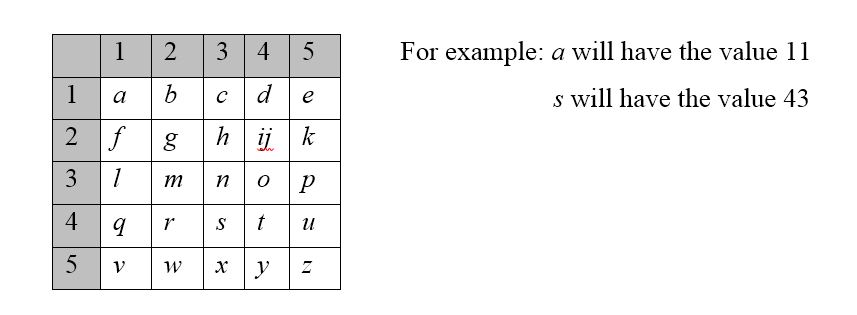
Table-1 Polybius square (Tabu S. Kondo, Leonard J. Mselle, 2013)

Some of the weaknesses/limitations of Polybius square include:

• Polybius has no key; therefore it can be easily broken.
• It only works for plain texts which contains only alphabets. There is no room for encrypting numbers and other characters such as punctuations and space.
• i and j are represented by the same pair numbers. This could create confusion when translating the cipher text to the original message.

The other popular historic cryptograph is the Caesar Cipher, which is invented by Julius Caesar around 58 B.C. Caesar shifted each letters by three and used it for his military command in order to make them appear meaningless should they get intercepted by the enemy (Khan-Academy, 2012). The number three in this case can be considered as a key which should be shared only between the sender and receiver. Often this type of cipher is implemented on a wheel device (See figure-2). If this technique is applied to the English language, the letter ain a message will be d and the letter s will be v. Once the message reached the receiver it will be converted to the original message by shifting each letters back by three.

Figure 2: Caesar wheel (Reynard, 1996)

Figure 2: Caesar wheel (Reynard, 1996)

In the English language the letter e is the most frequent letter followed by t. Therefore to break a cipher written in English using the frequency analysis, first the frequency of each letter in the cipher is counted. Then the most frequent letter in the cipher is considered as e and the distance of the shift is calculated. Based on the value of shift, the rest of the letters are then moved accordingly. The general idea is that when the most frequent letter in the cipher (in any language) is determined, it is easy to calculate how far the shift was from the most frequent letter.Caesar cipher method was used by military leaders for hundreds of years after Caesar. The simplest form of this type of substitution is easy to break. Example, for the 26 English letters there are only 26 shifts. Thus one can easily use the brute-force attack and exhaust all the possible options to get the original message. On the other hand if one-to-one substitution, commonly known as Monoalphabetic ciphers, is used there will be a possible combination of 26! (Factorial of 26) which equals to 403,291,461,126,605, 635,584,000,000 number of combinations (Ekert, 2005). In spite of it being used for such a long period of time, the weakness of Caesar cipher was first published after 800 years by an Arab mathematician Al-Kindi (800-873 A.D.) (Khan-Academy, 2012). Al-Kindi studied the Koran and discovered that Arabic has a characteristic letter frequency. By analysing the frequency of the letters in the language the message was written, Al-Kindi was able to break the Caesar cipher. His achievement is believed to be the birth of cryptanalysis – code breaking- (AAMT, 2012). It is possible to get the frequency of each letter in any language which is considered as the “finger print of the language”. For example if we scan the letters of any English book and count the frequency of each letter, we will be able get a fairly uniform frequency of each letter as shown in figure-3.

Figure 3: Frequency graph for English language (AAMT, 2012)

Figure 3: Frequency graph for English language (AAMT, 2012)

Throughout history more and more cryptography methods as well as cryptanalysis were and are being invented. Each of them has their own weakness and strengths. Moreover, the intrusion of digital systems also gives new dimension to the history of cryptography.